Objectives

The diploma in general engineering is a demanding, multidisciplinary training program that provides answers to the complex issues linked to the major transitions in business and society thanks to a systemic approach.
Internationally recognized, this program combines scientific and technical training with international and corporate experience through projects and internships. It thus ensures a deep understanding of contemporary challenges. Tomorrow's leaders and entrepreneurs, graduates exercise their skills in a wide range of professional sectors.
Program
A first year between common core and discovery of engineering professions

Common Core: a common generalist culture
The scientific, humanistic and economic disciplinary teaching constitute the essential baggage of the generalist engineer Centrale Lyon. The UEs followed by the entire graduating class, each group together a set of training activities that can combine lectures, tutorials, practical work and teamwork on case studies.
Study projects
In the first year, a scientific or technical problem is submitted to the student engineers by the teaching teams of the etablishment or in collaboration with partner companies and research laboratories.
The groups, made up of4 to 6 students, are supervised by a teaching team for everything to do with project management, engineering sciences and human and social sciences. The teaching team is made up of a scientific tutor, a communication advisor and a project management advisort.
The objectives of the study project are:
- confronting a complex problem with no single solution
- leading a team project
- seeking skills and information
- implementing means and obtaining results
- mastering written and oral communication
WEEX : Weeks of Engineering EXperience
WEEX (Weeks of Engineering EXperience) are three weeks offered during the core curriculum and dedicated to developing the global vision of a project. Students work on innovation issues in collaboration with partner companies or local players. They are tasked with proposing innovative solutions around societal issues(energy transition, waste treatment, mobility) through a pluri-disciplinary approach.
Students have to design a model, taking into account various parameters and managing any mechanical, acoustic, geographical or environmental hazards.... They interact, also learn to manage tensions, to confront risks. In this way, WEEX gives meaning to the core curriculum.
Execution internship
During the execution internship, the student trainee discovers and performs the work of an operator over a minimum four-week period. This internship is designed to introduce students to the workings of a company, the nature of execution work and the relationships between operators and managers.
A second year from general education to personalized career path

Common core: a common generalist culture
In the second year, engineering students finalize their common core teaching during the first semester (S7). A "UE d'approfondissement" (in-depth study) enables them to study a theme in greater depth in two different scientific UEs to be chosen from a total of 32, with a small number of students (24).
Application project
In 2nd year, the project activity continues in two different forms to choose from:
- The Industrial Application Project (PAi) enables 2nd year students to confront a project of an industrial nature. This involves a subject (technical, market analysis or intelligence) defined by a sponsoring company and handled under its supervision. Students are accompanied by a project advisor who guides them throughout the 7-month activity.
- The Research Application Project (PAr) constitutes a first individual research experience with personalized supervision in one of the École's laboratories.
One semester to choose from: elective pathway or international mobility
In the second year, students can choose 5 courses from nearly 60 on offer. It enables student-engineers to deepen the concepts seen in the core curriculum or to discover other disciplinary fields. The organization allows for strong specialization or a balanced path, depending on each student's project.
Engineering students can also choose to validate their second semester (S8) at a foreign university for 30 ECTS or equivalent. These exchanges can take place at one of Centrale Lyon's partner universities, under the Erasmus program or outside it.
Students can also follow a semester-long laboratory research project subject to validation of the project by a Centrale Lyon scientific correspondent professor.
The application internship
Conducted at the end of the second year, the application internship lasts a minimum of 3 months and must be completed by the start of the following academic year. The aim of the application internship is to introduce students to engineering professions through active integration into an engineering team.
The function performed and the work carried out correspond, over a relatively short period, to what is required of an engineer at the start of his or her career. It's also an opportunity to apply the knowledge and skills acquired at Centrale Lyon.
A third year à la carte
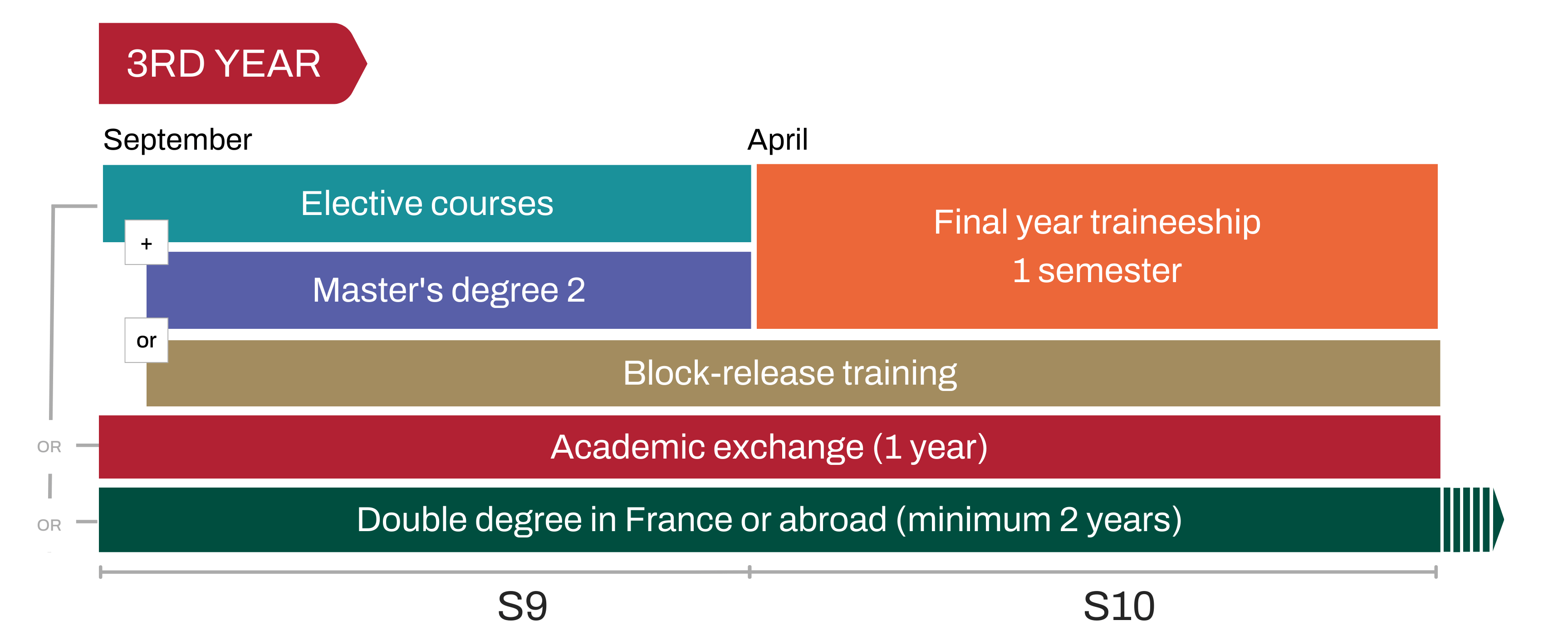
An à la carte pathway
The third year of the general engineering curriculum offers many pathway possibilities. Whether it's a more in-depth study of a particular sector, an academic exchange, or a double degree in France or abroad, each student builds his or her career path according to his or her professional project.
In the third year, students can pursue the elective path and customize their courses from among all the UE offered within Centrale Lyon.
9 COURSES TO CHOOSE from more than 50 themes
1 BUSINESS COURSE
- Consulting engineer
- Eco-design and innovation engineer
- Supply chain and business performance engineer
- Industrial and environmental risk management engineer
- Research engineer, innovation and development
- Intrapreneur and entrepreneurial engineer
1 SECTORAL COURSE
- Aeronautics
- Bioengineering for health
- Energy
- Physical for major transitions
- Ecological transition and territories
- Informatics
- Mathematics and decision-making
- Transport, mobility and decarbonation
At the end of the 2nd year, the student engineer now has the option of doing the 3rd year through the professionalization contract route. For student engineers, the professionalization contract enables them to:
- foster discovery of the professional environment through experimentation and hands-on experience over the course of a year, alternating with a company
- gain in maturity
- refine their life project and career choice
- develop experience before the end of their academic course
- acquire a dual skill set: a function in the company linked to the target profession and technical and sector-specific skills linked to the option.
For the company, it's an opportunity to benefit from the talent and skills of a Centrale Lyon student-engineer.
As part of its various partnerships with the Groupe des Écoles Centrale, the Collège d'ingénierie Lyon Saint-Étienne and emlyon business school, Centrale Lyon offers its students the opportunity to open up their fields of expertise and take their third year at another institution.
In addition, exchanges of courses within the curriculum are possible at member institutions of the CHELS.
Engineering students can take a double degree with one of the Etablishment's partner institutions in France or abroad. Some courses are accessible from the first year.
Going international
Engineering students must undertake international mobility to validate their curriculum. This mobility can take various forms:
- a semester or year of exchange
- a double degree
- an internship
- a gap year
Grandes Écoles double degrees
Thanks to prestigious partnerships, Centrale Lyon offers numerous double degree opportunities to its student-engineers, some of which are accessible as early as the first year.
Grandes Écoles double degrees
Thanks to prestigious partnerships, Centrale Lyon offers numerous double degree opportunities to its student-engineers, some of which are accessible as early as the first year.
Diplomas and certifications
This course delivers a national engineering diploma, controlled by the State and accredited by the Commission des Titres d'Ingénieur.



Admission requirements and application
The Centrale Lyon general engineering program is accessible via the CapECL integrated preparatory cycle. This 2-year curriculum provides intensive scientific training in mathematics and physics-chemistry. Students are brought together in a small class of 24 students with dedicated teachers for personalized follow-up.
Concours CentraleSupélec
The main admission route to Centrale Lyon is the CentraleSupélec competitive entrance exam. Students who pass this competitive entrance exam are admitted as student engineers.
Preparation for the competitive entrance exam generally takes place in the classes préparatoires aux grandes écoles (CPGE) scientific high schools. The level corresponds to a minimum of two years of preparation after the baccalauréat.
The competition is managed by the Service du Concours located at Centrale Supélec (SCEI): information, registration files, requests for transcripts, information on organization or progress, complaints...
Le Concours Universitaire des Écoles Centrale
General engineering training is open after a BAC +3 via the Concours Universitaire des Écoles Centrale (common recruitment route for the Écoles Centrale).
Who can apply?
It is open to students at the end of their Bachelor's degree course (L3) in countries operating with the LMD system, and to students at the end of their Bachelor's degree course in countries not using this system.
The bachelor's degrees opening up to the Concours Universitaire des Écoles Centrale are as follows: mathematics, mathematics-computing, mechanics and physics.
Places offered
The Écoles Centrale Group offers 75 places each year (including 20 offered by Centrale Lyon).
How to apply?
The admission procedure takes place in two stages:
- A pre-selection carried out on the basis of applications (around 300 candidates and almost 2/3 selected)
- A competitive examination comprising a written scientific test, an oral scientific test, an English test and then an interview.
As an international student, you can enrol in Centrale Lyon's general engineering programme to obtain an engineering degree or earn ECTS (European Credit Transfer System) credits.
Academic exchanges
With more than 140 academic exchange agreements, Centrale Lyon offers international students the opportunity to participate in an academic exchange (semester or year) or a dual degree programme for its general engineering programme. You must contact the registrar's office at your home institution to find out about admission requirements.
Discover our international partners
Double degree
As part of a partnership between your university and Centrale Lyon, you can enrol in a programme leading to a double degree:
- The Centrale Lyon engineering degree
- The degree from your home university
Exchange year (Master's 2 level)
You can spend a full year at Centrale Lyon, in your third year, choosing:
- A sector-specific specialisation option
- One of the professional tracks offered
Exchange semester (Master's 1 or 2 level)
You also have the option of coming for a semester, in your second or third year, in order to earn ECTS credits as part of your degree programme.
Admission via international competitive examination
Candidates who have not completed higher education in France and who are nominated by a secondary school in conjunction with the French Embassy may enrol in the international programme. As such, Centrale Lyon offers:
- 8 places for the MPC programme
- 1 place for the PC programme
- 1 place for the PSI programme
- 15 places for the MP programme
Discover the Centrale Supélec competition website
Auditor
It is also possible to attend classes as an auditor, without obtaining a degree or credits, under certain conditions.
Contact the International Relations Office
Tuition fees
Starting in the 2026 academic year, Centrale Lyon will implement a sliding scale for tuition fees for the entire engineering programme. Fees, which will now be calculated based on taxable income, will range from €1,613 to €4,113 per year. A full exemption is maintained for students receiving CROUS grants.












