Objectifs

Le diplôme d'ingénieur généraliste est une formation exigeante et pluridisciplinaire qui permet d'apporter des réponses aux enjeux complexes liés aux grandes transitions des entreprises et de la société grâce à une approche systémique.
Reconnu internationalement, ce programme combine formation scientifique et technique et expériences à l’international et en entreprise au travers de projets et de stages. Il assure ainsi une compréhension approfondie des défis contemporains. Leaders et entrepreneurs de demain, les diplômés exercent leurs compétences dans un large éventail de secteurs professionnels.
Programme
Une première année entre tronc commun et découverte des métiers de l'ingénieur

Tronc Commun : une culture généraliste commune
Les enseignements disciplinaires scientifiques, humanistes et économiques constituent le bagage indispensable de l'ingénieur généraliste Centrale Lyon. Les UE suivies par l’ensemble de la promotion, regroupent chacune un ensemble d’actions de formation pouvant allier des cours magistraux, des travaux dirigés, des travaux pratiques et des travaux d’équipe sur des études de cas.
Projets d’études
En première année, une problématique scientifique ou technique est soumise aux élèves-ingénieurs par les équipes pédagogiques de l'École ou en collaboration avec des entreprises partenaires et des laboratoires de recherche.
Les groupes, composés de 4 à 6 élèves, sont encadrés par une équipe pédagogique pour tout ce qui touche à la gestion de projet, aux sciences de l'ingénieur et aux sciences humaines et sociales. L'équipe pédagogique est composée constituée d'un tuteur scientifique, d'un conseiller en communication et d'un conseiller en gestion de projet.
Les objectifs du projet d'études sont :
- la confrontation à un problème complexe sans solution unique
- la conduite de projet en équipe
- la recherche de compétences et d'informations
- la mise en place de moyens et l'obtention de résultats
- la maîtrise de la communication écrite et orale
WEEX : Weeks of Engineering EXperience
Les WEEX (Weeks of Engineering EXperience) sont trois semaines intégrées au tronc commun, consacrées au développement d’une vision globale de projet. Durant ces périodes, les élèves-ingénieurs travaillent sur des problématiques d’innovation en collaboration avec des entreprises partenaires ou des acteurs locaux. Ils sont amenés à proposer des solutions innovantes à des enjeux de société tels que la transition énergétique, le traitement des déchets ou la mobilité, dans une approche résolument pluridisciplinaire.
Ils doivent concevoir un modèle intégrant différents paramètres, tout en anticipant et gérant d’éventuels aléas mécaniques, acoustiques, géographiques ou environnementaux. Ce travail les amène à interagir, à gérer les tensions et à se confronter aux risques inhérents à tout projet complexe.
Les WEEX donnent ainsi tout leur sens aux enseignements du tronc commun, en les ancrant dans des situations concrètes et collaboratives.
Stage d’exécution
Lors du stage d'exécution, l'élève stagiaire découvre et effectue le travail d’un opérateur sur une période de quatre semaines minimum. Ce stage vise à faire découvrir aux élèves le fonctionnement d'une entreprise, la nature du travail d'exécution et les relations entre opérateurs et cadres.
Une deuxième année de l'enseignement général à la personnalisation du parcours
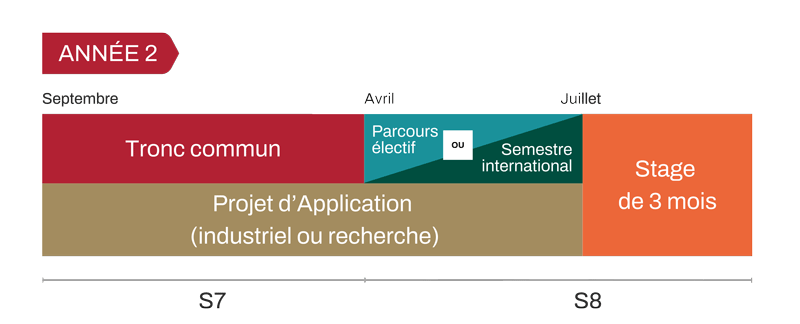
Tronc Commun : une culture généraliste commune
En 2e année, les élèves-ingénieurs terminent leur tronc commun au premier semestre (S7). Une unité d’enseignement d’approfondissement leur permet d’explorer un thème en profondeur à travers deux modules scientifiques au choix, parmi 32 proposés, dispensés en petits groupes de 24 élèves.
Projet d’application
En 2e année, l’activité de projet se poursuit sous deux formes au choix :
- Le Projet d’Application industriel (PAi) confronte les élèves à une problématique industrielle réelle. Le sujet, d’ordre technique, commercial ou stratégique, est proposé par une entreprise partenaire et suivi sous sa supervision. Les élèves sont accompagnés pendant les 7 mois du projet par un conseiller qui les guide dans leur démarche.
- Le Projet d’Application de recherche (PAr) offre une première expérience individuelle de la recherche, avec un encadrement personnalisé au sein d’un des laboratoires de l’École.
Un semestre au choix : parcours électif ou mobilité internationale
Au second semestre de 2ᵉ année (S8), les élèves peuvent choisir 5 cours parmi près de 60 proposés. Le parcours électif permet aux élèves-ingénieurs d'approfondir les notions vues en tronc commun ou de découvrir d'autres champs disciplinaires. L'organisation permet une spécialisation forte ou un parcours équilibré, selon le projet de chaque élève.
Au second semestre de 2ᵉ année (S8), les élèves-ingénieurs ont la possibilité de valider 30 ECTS ou équivalents dans une université étrangère.
Ces échanges s’effectuent dans le cadre d’un partenariat avec Centrale Lyon, que ce soit via le programme Erasmus ou hors programme, selon les accords bilatéraux en place.
Ils peuvent également choisir d’effectuer un semestre de recherche en laboratoire, sous réserve de validation du projet par un enseignant référent de Centrale Lyon.
Le stage d’application
Effectué en fin de deuxième année, le stage d'application dure au minimum 3 mois et doit être achevé à la rentrée universitaire suivante. L’objectif du stage d’application est de faire découvrir à l'élève les métiers de l'ingénieur par une intégration active dans une équipe d'ingénieurs.
La fonction exercée et le travail effectué correspondent, sur une période relativement courte, à ce qui est demandé à un ingénieur en début de carrière. C'est aussi l'occasion de mettre en application les connaissances et compétences acquises à Centrale Lyon.
Une troisième année à la carte
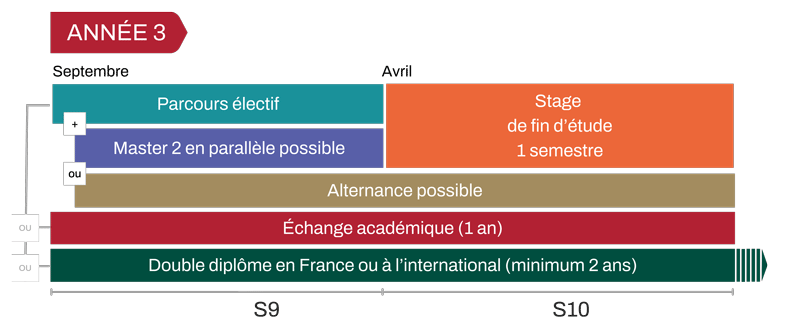
La troisième année du cursus ingénieur généraliste offre de nombreuses possibilités de personnalisation. Approfondissement sectoriel, échange académique ou double diplôme en France comme à l’international : chaque élève construit son parcours en cohérence avec son projet professionnel.
En troisième année, les élèves peuvent choisir de poursuivre leur formation à Centrale Lyon en construisant un parcours électif, personnalisé autour d’unités d’enseignement (UE) choisies parmi une large offre.
- 9 COURS AU CHOIX parmi plus de 50 thématiques
- + 1 APPROFONDISSEMENT MÉTIER, parmi les profils suivants :
- Ingénieur Consultant
- Ingénieur éco-conception et innovation
- Ingénieur Supply chain et performance de l'entreprise
- Ingénieur management des risques industriels et environnementaux
- Ingénieur recherche, innovation et développement
- Ingénieur intrapreneur et entrepreneur
- + 1 APPROFONDISSEMENT SECTORIEL, au choix parmi :
- Aéronautique
- Bio-Ingénierie de la santé
- Énergie
- Physique
- Transition écologique et territoires
- Informatique
- Mathématiques et décision
- Transports, mobilités et décarbonation
À l’issue de la 2e année, les élèves-ingénieurs ont la possibilité d’effectuer leur 3ᵉ année en alternance, sous contrat de professionnalisation. Cette voie offre de nombreux bénéfices :
- Découvrir le milieu professionnel par l’expérimentation et la mise en situation concrète
- Gagner en maturité et en autonomie
- Affiner son projet personnel et professionnel
- Développer une expérience significative avant la diplomation
- Acquérir une double compétence : une fonction en entreprise liée au métier visé, et des connaissances techniques approfondies liées à l’option suivie
Grâce à ses partenariats avec le Groupe des Écoles Centrale, le Collège d'ingénierie Lyon Saint-Étienne et emlyon business school, Centrale Lyon permet à ses élèves d’élargir leurs compétences en réalisant leur 3ᵉ année dans un autre établissement partenaire.
Des échanges de cours sont également possibles avec les établissements membres du CHELS (Collège des Hautes Études Lyon Sciences).
Les élèves-ingénieurs peuvent aussi choisir de suivre un double diplôme avec l’un des nombreux établissements partenaires de l’École, en France ou à l’étranger. Certains parcours sont accessibles dès la première année.
Partir à l'international
Les élèves-ingénieurs doivent effectuer une mobilité internationale pour valider leur cursus. Cette mobilité peut prendre différentes formes :
- un semestre ou une année d'échange
- un double diplôme
- un stage
- une césure
Doubles diplômes : Grandes Écoles
Grâce à des partenariats prestigieux, Centrale Lyon offre de nombreuses opportunités de double diplômes à ses élèves-ingénieurs accessibles, pour certains, dès la première année.
Doubles diplômes : licences, masters et à l’international
En parallèle de leur cursus, les élèves-ingénieurs peuvent valider une licence (mathématiques, physique ou économie), suivre un master 2 en dernière année, ou partir à l’international grâce à plus de 50 accords de double diplôme.
Diplôme et certifications
Cette formation délivre un diplôme national d'ingénieur, contrôlé par l’État et accrédité par la Commission des Titres d'Ingénieur.



Conditions d’accès et candidature
La formation ingénieur généraliste Centrale Lyon est accessible via le cycle préparatoire intégré CapECL. Ce cursus en 2 ans apporte une formation scientifique intensive en mathématiques et physique-chimie. Les étudiants sont rassemblés au sein d'un petite classe de 24 élèves avec des enseignants dédiés pour un suivi personnalisé.
Concours CentraleSupélec
La voie principale d'admission à Centrale Lyon est le concours CentraleSupélec. Les étudiants qui réussissent ce concours sont admis comme élèves-ingénieurs.
La préparation au concours s'effectue généralement dans les classes préparatoires aux grandes écoles (CPGE) scientifiques des lycées. Le niveau correspond à deux ans minimum de préparation après le baccalauréat.
Le concours est géré par le Service du Concours situé à Centrale Supélec (SCEI) : informations, dossiers d'inscriptions, demandes de relevés de notes, renseignements sur l'organisation ou le déroulement, réclamations...
Le Concours Universitaire des Écoles Centrale
La formation ingénieur généraliste est ouverte après un BAC +3 via le Concours Universitaire des Écoles Centrale (voie de recrutement commune aux Écoles Centrale).
Qui peut candidater ?
Le Concours Universitaire des Écoles Centrale s’adresse aux étudiants en dernière année de Licence ou d’un Bachelor conférant le grade de Licence, dans un cursus scientifique.
Les spécialités ouvrant au concours sont notamment :
- Mathématiques
- Mathématiques et informatique
- Mécanique
- Physique
Les candidats doivent avoir un solide bagage scientifique et une forte motivation pour intégrer une formation d’ingénieur généraliste.
Places offertes
Le Groupe des Écoles Centrale propose chaque année 75 places (dont 20 offertes par Centrale Lyon).
Comment candidater ?
La procédure d'admission se déroule en deux étapes :
- Une présélection effectuée sur dossier (300 candidats environ et près de 2/3 sélectionnés)
- Un concours comportant une épreuve scientifique écrite, une épreuve scientifique orale, un test d'anglais puis un entretien.
En tant qu’étudiant international, vous pouvez intégrer le cycle ingénieur généraliste de Centrale Lyon pour obtenir le diplôme d’ingénieur ou valider des crédits ECTS (European Credit Transfer System).
Plusieurs modalités d’admission et de séjour sont possibles
Double diplôme
Dans le cadre d’un partenariat entre votre université et Centrale Lyon, vous pouvez suivre une formation menant à un double diplôme :
- Le diplôme d’ingénieur de Centrale Lyon
- Le diplôme de votre université d’origine
Année d’échange (niveau Master 2)
Vous pouvez effectuer une année complète à Centrale Lyon, en 3ᵉ année, en choisissant :
- Une option d’approfondissement sectoriel
- Une filière métier parmi celles proposées
Semestre d’échange (niveau Master 1 ou 2)
Vous avez également la possibilité de venir pour un semestre, en 2ᵉ ou 3ᵉ année, afin de valider des crédits ECTS dans le cadre de votre cursus.
Admission via concours international
Si vous êtes étudiant d'une filière scientifique type MP, PC ou PSI, vous pouvez présenter le concours spécial du cycle international pour intégrer le programme ingénieur.
Auditeur libre
Il est enfin possible de suivre des enseignements en tant qu’auditeur ou auditrice libre, sans validation de diplôme ou de crédits, sous certaines conditions.
Frais d’inscription
Frais administratifs
- Frais d’inscription : 2613€
- CVEC : 103€ (gratuit pour les boursiers)
Vie quotidienne
Les frais de vie courante restant à charge sont en moyenne de 1 000 € par mois. Centrale Lyon met à la disposition de tous ses étudiants un service pour les aider dans leurs démarches.
Frais administratifs
- Frais d’inscription : 3 941€
- CVEC : 103€ (gratuit pur les étudiants en accord d’échange international)
Vie quotidienne
Les frais de vie courante restant à charge sont en moyenne de 1 000 € par mois. Centrale Lyon met à la disposition de tous ses étudiants un service pour les aider dans leurs démarches.












